Discrete Cosine Transform - Part 1
- Type 1 periodic extension
- Definition of DCT-1
- DFT of Type 1 periodic extension
- Type 2 periodic extension
- Definition of DCT-2
- DFT of Type 2 periodic extension
- Type 3 Periodic extension
- Definition of DCT-3
- Type 4 Periodic extension
- Definition of DCT-4
- Inverse Discrete Cosine Transform
- Inverse DCT 1
- Inverse DCT 2
- References
Recall the definition of even and odd functions: \begin{aligned}f(-x) = f(x) \ :even\ function \\ f(-x) = -f(x)\ :odd\ function.\end{aligned} As $cos(-x)=cos(x), sin(-x)=-sin(x)$, the cosine function is even and the sine function is odd.
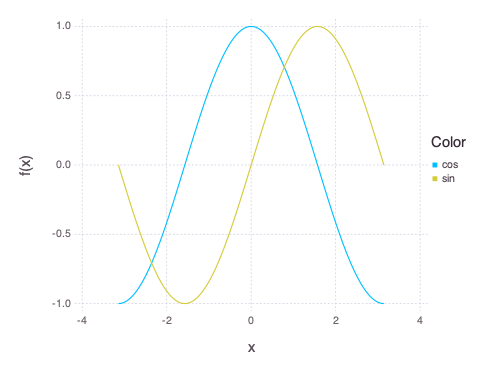
With the Discrete Fourier transform (DFT), we multiply a real signal $x[n]$ by the basis complex exponential $e^{j2\pi kn/N}$. This results in general complex valued transforms. The DCT is a transform where the basis sequences are cosines (using only the real part of $e^{j2\pi kn/N}$). This results in real valued transforms. The DCT inherits the even symmetry and periodic properties of $cos$ functions.
We start with a 4 point signal $x_o[n]$ as shown below.
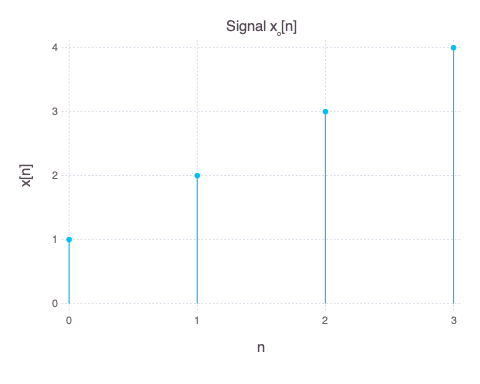
We next extend $x_o[n]$ such that it exhibits the even property (“cos like”) and extend copies of the new even signal with period T to achieve periodicity. There are many ways of doing this, one example of this is to mirror $x_o[n]$ over $n=0$ and then shifting copies of it for perodicity. The 4 common even periodically extension of the signal $x_o[n]$ are shown below.
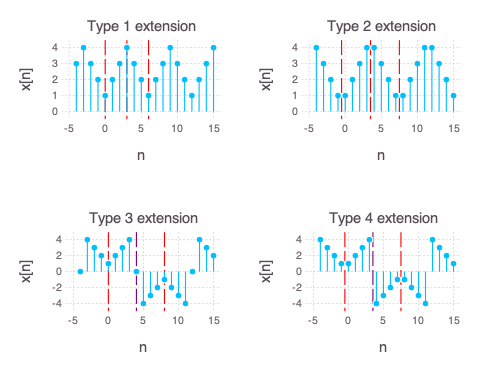
Type 1 periodic extension
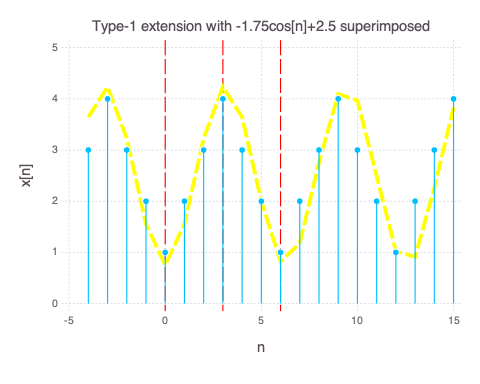
The Type 1 periodic extension is obtained by mirroring $x_o[n]$ about $n=0$ and then sliding the signal to n=3, 9, … The mirrored $x_o[n]$ + $x_o[n]$ signal has period 6 (2N-2). When we add the mirrored $x_o[n]$ + $x_o[n]$ together and then periodically extend them, the edge points (N=0, N-1) overlap. Hence, there is a scale of half at the edge points (N=0, N-1). Note that the resulting Type 1 periodic extension has a similar oscillatory cosine property. To see this, we plot an approximate $-1.75cos(n)+2.5$ envelop (yellow) over our signal. We can see from the yellow dashed line that
- It is even around 0, N-1, 2N-2… (In cos equivalent terms, 0, $\pi$, $2\pi$…). The red vertical dashed lines show even symmetry.
- There is a DC bias. This suggests that with our Type 1 periodic extension, in addition to the cosine component, we have a constant bias in the signal.
Definition of DCT-1
\(\begin{aligned}X_{DCT-1}[k] = \sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi nk }{N-1}) \\ for\ k=0...N-1 \\ where \ \alpha[n]=\begin{cases}\frac{1}{2}\ for\ n=0,N-1 \\ 1\ for\ n=1...N-2 \end{cases}\end{aligned}\)
Even/Odd Property:
- At n=0 & N-1, x[n] is even
- At k=0 & N-1, X[k] is even
DFT of Type 1 periodic extension
For notation simplicity here, let $x[n]=x_o[n]$, mirrored $x_o[n] = x[-n]$
\(\begin{aligned}
&Using\ the\ DFT\ definition: DFT\{x[n]\} = \sum_{n=0}^{N-1}x[n]e^{-j\omega k} \\
& 2N-2\ point\ DFT \{\alpha[n]x[n]+\alpha[n]x[-n]\} \\
&= \sum_{n=0}^{2N-3}\alpha[n]x[n]e^{-j2\pi nk/(2N-2)} + \sum_{n=0}^{2N-3}\alpha[n]x[-n]e^{j2\pi nk/(2N-2) } \\
&= \sum_{n=0}^{2N-3}\alpha[n]x[n]e^{-j2\pi nk/(2N-2)} + \sum_{n=0}^{2N-3}\alpha[n]x[n]e^{j2\pi nk/(2N-2) } \\
&(using\ x[n]=x[-n]\ property) \\
&= \sum_{n=0}^{N-1}\alpha[n]x[n]e^{-j2\pi nk/(2N-2)} + \sum_{n=0}^{N-1}\alpha[n]x[n]e^{j2\pi nk/(2N-2) } \\
&(using\ the\ fact\ that\ N-1\ points\ are\ zeros\ (padding)) \\
&= 2\underbrace{
\sum_{n=0}^{N-1}\alpha[n]x[n]cos(\frac{\pi nk}{N-1})}_{\text{$X_{DCT-1}$[k]}} \qquad \qquad \text{(1)}
\end{aligned}\)
Type 2 periodic extension
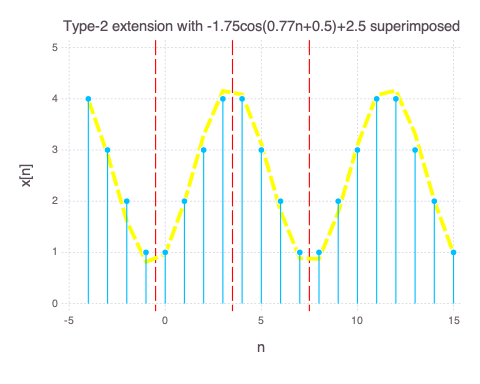
The Type 2 periodic extension is obtained by mirroring $x_o[n]$ about $n=-0.5$ and then sliding the signal to n=3.5, 11.5, … The $x_o[-n-1]$ + $x_o[n]$ signal has period 8 (2N). Unlike the Type 1, when we add $x_o[-n-1]$ + $x_o[n]$ together and then periodically extend them, there is no overlap. Note that the resulting Type 2 periodic extension has a similar oscillatory cosine property. To see this, we plot an approximate $-1.75cos(0.77n+0.5)+2.5$ envelop (yellow) over our signal. We can see from the yellow dashed line that
- It is even around -0.5, N-0.5, 2N-0.5… (In cos equivalent terms, 0, $\pi$, $2\pi$…). The red vertical dashed lines show even symmetry.
- There is a DC bias.
Definition of DCT-2
\(\begin{aligned}X_{DCT-2}[k] =\sum_{n=0}^{N-1} x[n]cos(\frac{\pi k (n+\frac{1}{2}) }{N}) \\ for\ k=0...N-1 \ \end{aligned}\)
Even/Odd Property:
- At n=-0.5 & N-0.5, x[n] is even
- At k=0, X[k] is even
- At k=N, X[k] is odd
This is the most commonly used DCT definition and is also known as the DCT.
DFT of Type 2 periodic extension
For notation simplicity here, let $x[n]=x_o[n]$, mirrored $x_o[n] = x[-n-1]$
\(\begin{aligned}
&Using\ the\ DFT\ definition: DFT\{x[n]\}=\sum_{n=0}^{N-1}x[n]e^{-j\omega k}\\
& 2N\ point\ DFT\{x[n]+x[-n-1]\}\\
&= \sum_{n=0}^{2N-1}x[n]e^{-j2\pi nk/(2N)} + \sum_{n=0}^{2N-1}x[-n-1]e^{j2\pi (n+1)k/(2N) }\\
&= \sum_{n=0}^{2N-1}x[n]e^{-j2\pi nk/(2N)} + e^{j2\pi k/(2N) }\sum_{n=0}^{2N-1}x[n]e^{j2\pi nk/(2N) }\\
&(using\ x[n]=x[-n-1]\ property)\\
&= e^{j\pi k/2N}[e^{-j\pi k/2N}\sum_{n=0}^{N-1}x[n]e^{-j2\pi nk/(2N)} + e^{j\pi k/2N}\sum_{n=0}^{N-1}x[n]e^{j2\pi nk/(2N) }]\\
&(using\ the\ fact\ that\ N\ points\ are\ zeros\ (padding))\\
&= e^{j\pi k/2N}[\sum_{n=0}^{N-1}x[n]e^{-j\pi (2n+1)k/(2N)} + \sum_{n=0}^{N-1}x[n]e^{j\pi (2n+1)k/(2N) }]\\
&= 2e^{j\pi k/2N}\underbrace{
\sum_{n=0}^{N-1}x[n]cos(\frac{\pi (2n+1)k}{2N})}_{\text{$X_{DCT-2}[k]$}} \qquad \qquad \text{(2)}
\end{aligned}\)
Type 3 Periodic extension
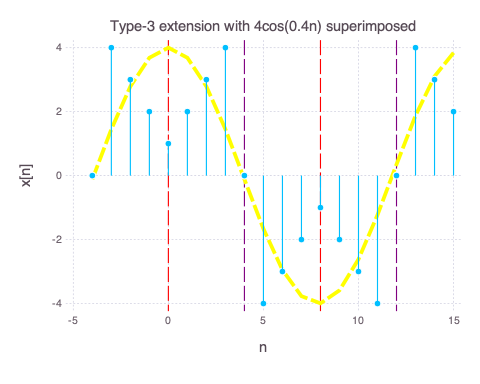
The Type 3 periodic extension is obtained by mirroring $x_o[n]$ about $n=0$ and then sliding the signal to n=5, 13, … The overall signal has period 16 (4N). Like the Type 1, when we add $x_o[-n]$ + $x_o[n]$ together and then periodically extend them, there is overlap at n=0. However at n=4 & n=12, there is a zero crossing and signal is flipped along n-axis. Note that the resulting Type 3 periodic extension has an oscillatory cosine property. To see this, we plot an approximate $4cos(0.4n)$ envelop (yellow) over our signal.
- We can see from the red dashed line that it is even around 0, 8… (half cycle) (In cos equivalent terms, 0, $\pi$, $2\pi$…).
- The vertical purple dashed lines show odd symmetry. (In cos equivalent terms, $\pi/2$, $3/2\pi$…)
- There is no DC bias.
Definition of DCT-3
\(\begin{aligned}X_{DCT-3}[k] =\sum_{n=0}^{N-1} \alpha[n] x[n]cos(\frac{\pi (k+\frac{1}{2})n }{N}) \\ for\ k=0...N-1 \\ where\ \alpha[n]=\begin{cases}\frac{1}{2}\ for\ n=0 \\ 1\ for\ n=1,...N-1\end{cases} \end{aligned}\)
Type 4 Periodic extension
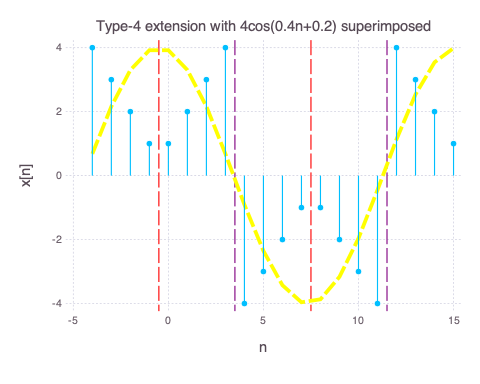
The Type 4 periodic extension is obtained by mirroring $x_o[n]$ about $n=-0.5$ and then sliding the signal to n=4, 12, … The overall signal has period 16 (4N). There is no overlaps unlike the DCT-3. Note that the resulting Type 4 periodic extension has an oscillatory cosine property. To see this, we plot an approximate $4cos(0.4n+0.2)$ envelop (yellow) over our signal.
- We can see from the red dashed line that it is even around -0.5, 7.5… (half cycle) (In cos equivalent terms, 0, $\pi$, $2\pi$…).
- The vertical purple dashed lines show odd symmetry. (In cos equivalent terms, $\pi/2$, $3/2\pi$…)
- There is no DC bias.
Definition of DCT-4
\(\begin{aligned}X_{DCT-4}[k] =\sum_{n=0}^{N-1} x[n]cos(\frac{\pi (k+\frac{1}{2}) (n+\frac{1}{2}) }{N})\\ for\ k=0...N-1\end{aligned}\)
Inverse Discrete Cosine Transform
Inverse DCT 1
To reconstruct $x[n]$ from $X_{DCT-1}[k]$ we can use the 2N-2 Inverse DFT formula and apply on $\text{(1)}$ \(\begin{aligned} &\frac{1}{2N-2}\sum_{k=0}^{2N-3}2X_{DCT-1}[k]e^{j2\pi kn/2N-2}\\ &=\frac{2}{2N-2}\sum_{k=0}^{2N-3}\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi nk }{N-1})e^{j2\pi kn/2N-2}\\ &=\frac{2}{2N-2}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi nk }{N-1})e^{j2\pi kn/2N-2} +\frac{2}{2N-2}\sum_{k=N}^{2N-3}\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi n(2N-2-k) }{N-1})e^{j2\pi n(2N-2-k)/2N-2}\\ &=\frac{2}{2N-2}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi nk }{N-1})e^{j2\pi kn/2N-2} +\frac{2}{2N-2}\sum_{k=N}^{N-1}\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi n(-k) }{N-1})e^{j2\pi n(-k)/2N-2}\\ &=\frac{2}{2N-2}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi nk }{N-1})[e^{j2\pi kn/2N-2}+e^{-j2\pi kn/2N-2}]\\ &=\frac{2}{2N-2}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi nk }{N-1})[2cos(\frac{\pi nk }{N-1})]\\ &=\frac{2}{N-1}\sum_{k=0}^{N-1}\underbrace{\sum_{n=0}^{N-1}\alpha[n] x[n]cos(\frac{\pi nk }{N-1})}_{\text{$X_{DCT-1}[k]$}}cos(\frac{\pi nk }{N-1})\\ \end{aligned}\)
\[\begin{aligned} IDCT-1 = \frac{2}{N-1}\sum_{k=0}^{N-1}X_{DCT-1}[k]cos(\frac{\pi nk }{N-1}) \\ for\ k=0...N-1 \end{aligned}\]Inverse DCT 2
To reconstruct $x[n]$ from $X_{DCT-2}[k]$ we can use the 2N Inverse DFT formula and apply on $\text{(2)}$ \(\begin{aligned} &\frac{1}{2N}\sum_{k=0}^{2N}X[k]e^{j2\pi kn/2N}\\ &=\frac{1}{2N}\sum_{k=0}^{2N}\sum_{n=0}^{N-1}2e^{j\pi k}x[n]cos(\frac{\pi k (n+\frac{1}{2}) }{N})e^{j2\pi kn/2N}\\ &=\frac{1}{N}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}x[n]cos(\frac{\pi k (n+\frac{1}{2}) }{N})e^{j\pi k(2n+1)/2N} +\frac{1}{N}\sum_{k=N}^{2N-1}\sum_{n=0}^{N-1}x[n]cos(\frac{\pi (2N-k) (n+\frac{1}{2}) }{N})e^{j\pi (2N-k)(2n+1)/2N}\\ &=\frac{1}{N}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}x[n]cos(\frac{\pi k (n+\frac{1}{2}) }{N})e^{j\pi k(2n+1)/2N} +\frac{1}{N}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}x[n]cos(\frac{\pi (-k) (n+\frac{1}{2}) }{N})e^{j\pi (-k)(2n+1)/2N}\\ &=\frac{1}{N}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}x[n]cos(\frac{\pi k (n+\frac{1}{2}) }{N})[e^{j\pi k(2n+1)/2N}+e^{-j\pi k(2n+1)/2N}]\\ &=\frac{1}{N}\sum_{k=0}^{N-1}\sum_{n=0}^{N-1}x[n]cos(\frac{\pi k (n+\frac{1}{2}) }{N})[e^{j\pi k(2n+1)/2N}+e^{-j\pi k(2n+1)/2N}]\\ &=\frac{2}{N}\sum_{k=0}^{N-1}\underbrace{\sum_{n=0}^{N-1}x[n]cos(\frac{\pi k (n+\frac{1}{2}) }{N})}_{\text{$X_{DCT-2}[k]$}}cos(\frac{\pi k(2n+1)}{2N})\\ \end{aligned}\)
\[\begin{aligned} IDCT-2 = \frac{2}{N}\sum_{k=0}^{N-1}X_{DCT-1}[k]cos(\frac{\pi k (n+\frac{1}{2})}{N})\\ for\ k=0...N-1\end{aligned}\]References
- Discrete-Time Signal Processing Third Edition Alan V. Oppenheim Ronald W. Schafer